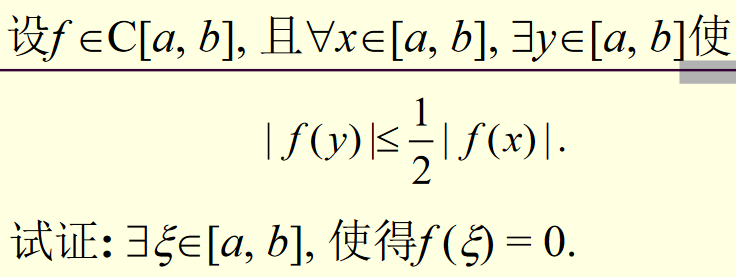MA.2.2 闭区间上连续函数的性质

#闭区间连续函数有界性 #闭区间连续函数最值性 #闭区间连续函数介值性 #闭区间连续函数零值性 #一致连续性

三值 + 一有界 + 一致连续

闭区间连续函数零值性

#零值定理

$若 f \in C [a, b], f (a) \cdot f (b) < 0, 则 \exists ξ \in (a, b), 使 f (ξ) = 0$

理解：连续+异号=存在零点

证明思路：

证明使用 #区间套定理 + 二分法

保持：区间端点值异号、闭区间、连续

闭区间连续函数介值性

#介值定理

$若 f \in C [a, b], f (a) < f (b), 则对 \forall μ \in (f (a), f (b)), \exists ξ \in (a, b), 使 f (ξ) = μ$

理解：两个端点值之间必存在

Corollary

$设 I 为区间, f (x) \in C (I) \Rightarrow f (I) 也是区间$
逆命题在特殊情况（单调，见下）成立
理解：连续函数定义域连续->值域连续

简证：

$\forall y_{1} < y_{2} \in f (I), \exists x_{1}, x_{2} \in I,$
$不妨设 x_{1} < x_{2}, f (x_{1}) = y_{1}, f (x_{2}) = y_{2}$
$∵ f (x) \in C [x_{1}, x_{2}], ∴ \forall μ \in (y_{1}, y_{2})$
根据 #介值定理

#介值定理

$若 f \in C [a, b], f (a) < f (b), 则对 \forall μ \in (f (a), f (b)), \exists ξ \in (a, b), 使 f (ξ) = μ$

理解：两个端点值之间必存在

$\exists ξ \in (x_{1}, x_{2}), 使 f (ξ) = μ$
$∴ [y_{1}, y_{2}] \subset f (I)$
$再由 y_{1}, y_{2} 任意性知 : f (I) 为区间$

Corollary

$设 f \in C [a, b] 且 f 存在反函数, 则 f 严格单调$

理解：否则不是单射

证明思路：

证明使用反证法，此时在端点与函数驻点之间运用 #介值定理，必定能找到两个 $y$ 与 $x$ 对应

任何奇次多项式至少有一个实零点

见笔记

Lemma

$若区间 I 上单调函数 φ 的值域为区间，则 φ \in C (I)$

理解：单调连续函数无间断=值域为区间

简证：

使用反证法，假设单调递增、 $x_{0}$ 间断，则在间断的去心邻域 $\overset{˚}{U} (x_{0}, δ)$ 有界（左右端点函数值）
由 #单调函数单侧极限定理
$φ (x_{0} - 0) = sup f (x_{0} - δ, x_{0})$ ,
$φ (x_{0} + 0) = inf f (x_{0}, x_{0} + δ)$
$∴ φ (x_{0} - 0) \leq φ (x_{0}) \leq φ (x_{0} + 0)$
$由间断知 : 等号不能同时取得, 即 φ (x_{0} - 0) < φ (x_{0} + 0)$
$∵ φ (x_{0}) {\begin{cases} \leq φ (x_{0} - 0) x < x_{0} \\ \geq φ (x_{0} + 0) x > x_{0} \end{cases}$
$∴ (φ (x_{0} - 0), φ (x_{0} + 0)) 中至多含 φ (I) 中一点，即 φ (x_{0})$
P.S. 至多： $当 φ (x_{0}) 与某一侧极限相等 / 连续时则不含有点$
$∴ φ (I) 非区间, 矛盾$

#反函数连续性

$若函数 f (x) 在区间 I 严格单调且连续, 记 J = f (I),$ $则其反函数 f^{- 1} 在区间 J 上连续$

证明如下：

非常优雅的证明:
$首先, f^{- 1} 在 J 上严格单调$
$其次, ∵ f \in C (I), 由$ 推论 $知 : J = f (I) 为区间$
$且, f^{- 1} 的值域 I 也为区间$
$由$ 引理 $知 : f^{- 1} 在 J 上连续$

Example

证明： $lim_{x \to 0} : \frac{\arcsin x}{x} = 1$ , $lim_{x \to 0} : \frac{\arctan x}{x} = 1$

闭区间连续函数有界性

#闭区间连续函数有界性

$若 f \in C [a, b], 则 f 在 [a, b] 上有界$

证明如下

使用反证法： $若 f 在 [a, b] 无界, 即 :$
$\forall M > 0, \exists x_{M} \in [a, b],$ $使 | f (x_{M}) | > M$

$取 M = 1,$ $\exists x_{1} \in [a, b],$ $使 f (x_{1}) > M$
$取 M = 2,$ $\exists x_{2} \in [a, b],$ $使 f (x_{2}) > M$
$以此类推$
$取 M = n,$ $\exists x_{n} \in [a, b],$ $使 f (x_{n}) > M$

$运用$ #BW定理

#BW定理列紧性定理致密性定理

有界数列必存在收敛子列
可以是多个极限不同的数列

$由于 x_{n} \in [a, b] 有界,$ $\exists x_{n_{k}} \in x_{n}$
$有 lim_{k \to \infty} f (x_{n_{k}}) = \infty$
$∵ f (x_{M}) > M,$ $∴ | f (x_{n_{k}}) | > x_{n_{k}} \geq k,$
$∴ lim_{k \to \infty} f (x_{n_{k}}) = \infty$

由 #连续函数极限的穿越

#连续函数极限的穿越

$若 f (x)$ $连续$ $, 则 lim 和 f 可交换位置$

$lim_{k \to \infty} f (x_{n_{k}}) = f (lim_{k \to \infty} x_{n_{k}}) = f (x_{0}) = \infty$
$函数无意义,$ $矛盾$

另：若换成开区间后不成立
例如： $x_{0} = a 时,$ $函数取值无意义,$ $lim 不可穿越$

闭区间连续函数最值性

#闭区间连续函数最值性

$若 f \in C [a, b],$ $则 f 在 [a, b] 上有最大、最小值,$ $即 \exists ξ_{1},$ $ξ_{2} \in [a, b],$ $使得$

f (ξ_{1}) = m = min_{x \in [a, b]} f (x), f (x i_{2}) = M = max_{x \in [a, b]} f (x)

证明：

构造辅助函数
由 #闭区间连续函数有界性

#闭区间连续函数有界性

$若 f \in C [a, b], 则 f 在 [a, b] 上有界$

知 $值域 f ([a, b]) 非空、 f 有界$
$\Rightarrow f ([a, b]) 有 sup, inf$
根据 #确界原理 , $存在上下确界$
$M = sup f ([a, b]) \in R$
$下证 : 上确界 M \in f ([a, b]), 即可证有最大值$
反证法： $若 M \notin f ([a, b]),$ $则 \forall x \in [a, b]$
$有 M > f (x)$
$令 F (x) = \frac{1}{M - f (x)}$ Tips: $\frac{1}{C} \in C$
$则 F \in C [a, b]$
根据 #闭区间连续函数有界性
$\exists β > 0, 使 \forall x \in [a, b],$ $有$
$F (x) = \frac{1}{M - f (x)} < β$
$∴ f (x) < M - \frac{1}{β} < M$
$故 M - \frac{1}{β} 也为上界,$ $与 M = sup f ([a, b]) 矛盾$

Corollary

$设 f \in C [a, b],$ $则值域 f ([a, b]) 是闭区间$

理解：闭区间 $\to$ 闭区间

#连续收敛函数有界性

$设 f \in C (R),$ $且 lim_{x \to \infty} f (x) = A \in R,$ $证明 : f 有界$

证明思路：

证明远处带状区域有界： $取 ε_{0} = 1 \Rightarrow | f (x) | < | A | + 1,$ $(| x | > | X |)$
证明中间有界：
$当 x \in [- X, X],$
根据 #闭区间连续函数有界性

#闭区间连续函数有界性

$若 f \in C [a, b], 则 f 在 [a, b] 上有界$

$∴ | f (x) | < B$
$\Rightarrow M = max {| A | + 1, B},$ $\forall x \in R,$ $| f (x) \leq M$

Example

Pasted image 20231101171406.png

Proposition

$设 f \in C [a, b],$ $M (x) 是 f 在区间 [a, x] (a \leq x \leq b) 上的最大值,$ $证明 :$ $$\lim\limits_{x\to a^{+}}M(x)=f(a)$$

简证：

$∵ lim_{x \to a^{+}} f (x) = f (a)$
$∴ \forall ε > 0,$ $\exists δ > 0,$ $\forall a \leq t < a + δ 有$
$| f (t) - f (a) | < ε \dots (*)$
由 #闭区间连续函数最值性

#闭区间连续函数最值性

$若 f \in C [a, b],$ $则 f 在 [a, b] 上有最大、最小值,$ $即 \exists ξ_{1},$ $ξ_{2} \in [a, b],$ $使得$
$f (ξ_{1}) = m = min_{x \in [a, b]} f (x), f (x i_{2}) = M = max_{x \in [a, b]} f (x)$

$\exists ξ_{x} \in [a, x] \subset [a, a + δ]$
$使 M (x) = f (ξ_{x}) \dots (* *)$
$由 (*), (* *)$
$| M (x) - f (x) | = | f (ξ_{x}) - f (a) | < ε$

一致连续性

$f \in U . C (I)$

#一致连续性

$设 f 在区间 I 上有定义,$ $若 \forall ε > 0,$ $\exists δ > 0,$ $\forall x^{'}, x^{″} \in I,$ $且 | x^{'} - x^{″} | < δ, 有$

| f (x^{'}) - f (x^{″}) | < ε

$则称 f 在 I 上一致连续, 记为 f \in U . C (I)$

非逐点定义：整体定义

一致连续与连续的关系及几何意义

函数极限的 #epsilon-delta定义

$\forall ε > 0, \exists δ > 0, 当 0 < | x - x_{0} | < δ 时有$
$| f (x) - l | < ε$
$则记为$
$lim_{x \to x_{0}} f (x) = l 或 f (x) \to l (x \to x_{0})$

左右单侧极限同理可得

#一致连续性

$设 f 在区间 I 上有定义,$ $若 \forall ε > 0,$ $\exists δ > 0,$ $\forall x^{'}, x^{″} \in I,$ $且 | x^{'} - x^{″} | < δ, 有$
$| f (x^{'}) - f (x^{″}) | < ε$
$则称 f 在 I 上一致连续, 记为 f \in U . C (I)$

非逐点定义：整体定义

一致连续是比连续更强的一种连续。强在何处呢？强在有一个共同的δ

几何意义

保证在整个区间内无陡峭处

保证平滑, 不出现强烈震荡及无穷

对比：

f \in U . C (I)

与 #连续的epsilon-delta表述的差异

连续的ε-δ表述
$\forall x^{'} \in I, \forall ε > 0, \exists δ (ε, x^{'}) > 0, \forall x^{″} \in I 且 | x^{'} - x^{″} | < δ, 有$

| f (x^{'}) - f (x^{″}) | < ε

一致连续性：加强
$\forall ε > 0, \exists δ (ε) > 0, \forall x^{'} \in I, \forall x^{″} \in I 且 | x^{'} - x^{″} | < δ, 有$

| f (x^{'}) - f (x^{″}) | < ε

一致连续性的否定

$\exists ε > 0, \forall δ > 0 (不具备可操作性), \forall x^{'} \in I, \exists x^{″} \in I 且 | x^{'} - x^{″} | < δ, 有$

| f (x^{'}) - f (x^{″}) | > ε

#不一致连续肯定叙述

$\exists ε_{0} > 0, \exists x_{n}^{'}, x_{n}^{″} \in I :$ $lim_{n \to \infty} (x_{n}^{'} - x_{n}^{″}) = 0, 但$ $| f (x_{n}^{'}) - f (x_{n}^{″}) | \geq ε_{0}$

理解：自变量接近，函数值不接近

证明：

$取 ε_{1} = 1, \exists ε_{0} > 0, x_{1}^{'}, x_{1}^{″} \in I 且 | x_{1}^{'} - x_{1}^{″} | < \frac{1}{n}$ $\Rightarrow lim_{n \to \infty} (x_{1}^{'} - x_{1}^{″}) = 0, 有$
$f (x_{1}^{'}) - f (x_{1}^{″}) \geq ε_{0}$
$⇕$
$取 ε_{n} = \frac{1}{n}, \exists ε_{0} > 0, x_{n}^{'}, x_{n}^{″} \in I 且 | x_{n}^{'} - x_{n}^{″} | < \frac{1}{n}$ $\Rightarrow lim_{n \to \infty} (x_{n}^{'} - x_{n}^{″}) = 0, 有$
$f (x_{n}^{'}) - f (x_{n}^{″}) \geq ε_{0}$

Example

$设 f (x) = a x + b, 证明 f \in U . C (R)$

证明： $\forall ε > 0, 取 δ = \frac{ε}{| a | + 1}, \forall x^{'}, x^{″} \in R$
$且 | x^{'} - x^{″} | < δ 时, 有$
$\begin{aligned} | f (x^{'}) - f (x^{″}) | \\ = | a | | x^{'} - x^{″} | \\ < | a | \cdot \frac{ε}{| a | + 1} \\ < | a | \cdot \frac{ε}{| a |} \\ = ε \end{aligned}$

思考: 震荡
$证明 f (x) = \sin \frac{1}{x} 在 (0, 1) 内不一致连续$

证明： $取 ε_{0} = 1, 令 x_{n}^{'} = \frac{1}{2 n π}, x_{n}^{″} = \frac{1}{2 n π + \frac{π}{2}} \in (0, 1)$
$lim_{n \to \infty} (x_{n}^{'} - x_{n}^{″}) = 0, 但$ $| f (x_{n}^{'}) - f (x_{n}^{″}) | = 1$

$证明 f (x) = x^{2} 在 R 上不一致连续$

证明： $取 ε_{0} = 1, 令 x_{n}^{'} = \sqrt{n}, x_{n}^{″} = \sqrt{n + 1} \in (0, 1)$
$lim_{n \to \infty} (x_{n}^{'} - x_{n}^{″}) = 0, 但$ $| f (x_{n}^{'}) - f (x_{n}^{″}) | = 1$

或

$令 x_{n}^{'} = n, x_{n}^{″} = n + \frac{1}{n}, 下略$

#Cantor定理

$f \in C [a, b], \Rightarrow f \in U . C [a, b]$

证明：

$若 f \notin U . C [a, b],$ $即 \exists ε_{0} > 0, x_{n}^{'}, x_{n}^{″} \subset [a, b],$ $满足 lim_{n \to \infty} (x_{n}^{'} - x_{n}^{″}) = 0$
$但 | f (x_{n}^{'}) - f (x_{n}^{″}) | > ε_{0}$
$∵ {x_{n}^{'}} 有界$
根据 #BW定理

#BW定理列紧性定理致密性定理

有界数列必存在收敛子列
可以是多个极限不同的数列

$\exists {x_{n_{k}}^{'}} \in {x_{n}^{'}} 收敛,$
$lim_{k \to \infty} x_{n_{k}} = x_{0} \in [a, b]$
$而 lim_{k \to \infty} x_{n_{k}}^{″} = lim_{k \to \infty} [(x_{n_{k}}^{″} - x_{n_{k}}^{'} + x_{n_{k}}^{'}]$ #添项
$∵ | f (x_{n_{k}}^{'}) - f (x_{n_{k}}^{″}) | \geq ε_{0} (\forall k \in N_{+})$
使用 #连续函数极限的穿越
$\begin{aligned} ∴ ε_{0} & \leq lim_{k \to 0} | f (x_{n_{k}}^{'}) - f (x_{n_{k}}^{″}) | \\ = | lim_{k \to 0} f (x_{n_{k}}^{'}) - f (x_{n_{k}}^{″}) | \\ = | f (lim_{k \to 0} x_{n_{k}}^{'}) - f (lim_{k \to 0} x_{n_{k}}^{″}) | \\ = | f (x_{0}) - f (x_{0}) | \\ = 0 \end{aligned}$

不适用于存在开的区间
- $\sin \frac{1}{x} 在 (0, 1) 连续, 但 \notin U . C (0, 1)$
- $x^{2} 在 [0, + \infty) 连续, 但 \notin U . C (0, 1)$

Theorem

$设 f \in C (a, b), 则$
$f \in U . C (a, b) \Leftrightarrow f (a + 0), f (b - 0) 存在$

理解:
一致连续=端点不陡峭=单侧极限存在

证明:

$\Rightarrow$
$∵ f \in C (a, b)$
$∴ \forall ε > 0, \exists δ > 0, \forall x^{'}, x^{″} \in (a, b), | x^{'} - x^{″} | < δ, 有$
$| f (x^{'}) - f (x^{″}) | < ε$
$∴ \forall x^{'}, x^{″} \in (a, a + δ) : | x^{'} - x^{″} | < ε$
使用 #Cauchy判别准则

Theorem #Cauchy判别准则

$lim_{x \to x_{0}} f (x) 存在 \Leftrightarrow$
$\forall ε > 0, \exists δ > 0, \forall x^{'}, x^{″} \in \overset{˚}{U} (x_{0}, δ) :$ $| f (x^{'}) - f (x^{″}) | < ε$
其他五种极限不再赘述

$∴ \exists f (a + 0)$
$同理, \exists f (b - 0)$

$\Leftarrow$
"补充定义"
$F (x) := {\begin{cases} f (a + 0), & x = a \\ f (x), & x \in (a, b) \\ f (b - 0), & x = b \end{cases}$
$∴ lim_{x \to a^{+}} f (x) = f (a + 0) = F (a)$
$类似地, lim_{x \to b^{-}} f (x) = f (b - 0) = F (b)$
$∴ F 在 x = a 右连续, x = b 左连续, 且 x \in C (a, b)$
$∴ F \in C [a, b]$
由 #Cantor定理
$F \in U . C [a, b] \to F \in U . C (a, b)$

Example

判断 $f \overset{?}{\in} U.C (I)$
$f (x) = x \sin \frac{1}{x}, x \in (0, + \infty)$
$f (x) = \frac{\sin x}{x}, x \in (0, + \infty)$
$f (x) = \frac{1}{x} \sin \frac{1}{x}, x \in (0, 1)$
$f (x) = s i n (x^{2}), x \in R$

Bonus:

证 明 \sin (x^{2}) 非 周 期 函 数

Proposition

$若 f \in C (a, + \infty), 且 x \to \infty 时有极限$ $\Rightarrow$ $f \in U . C (a, + \infty)$

Proposition

$若 f \in C (R) 且为周期函数$ $\Rightarrow$ $f \in U . C (R)$

理解：连续周期函数必一致连续

三值 + 一有界 + 一致连续

闭区间连续函数零值性

闭区间连续函数介值性

闭区间连续函数有界性

闭区间连续函数最值性

一致连续性

f∈U.C(I)

一致连续性的否定

$f \in U . C (I)$